|
| We are in the year 32 758. Jaro, 23 years, lives with his
wife and her small 6-year-old daughter on the planet Véga. Regrettably,
one day one announces him that he caught a terrible disease. The
only remedy to look after him is a plant, Géromia
Netsulum, who grows only on the planet Formalhault. Jaro,
having looked on the galactic atlas, notice that Formalhault is in just a
little less than 10 Véga's light years. In spite of his spaceship
capable of going to the speed of 99,5 % of that of the light, Jaro is well
afraid that the time of journey is too long. In this rhythm, he will need
10 years to go on Formalhault.
Nevertheless, he knows very
well that in this speed, he is not going to be any more in the same
dimension as the inhabitants of Véga and that he can divide the time of
the journey and the distance separating both planets by a factor g (gamma) thanks to famous formula which he taught to
the school when he all was small:
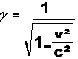 V being the speed of its vessel
C the speed of
light
For this scenario we shall have this formula:
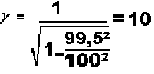
So at the speed of 99,5 % of the light, the spaceship, his occupants,
all the objects as he contains including the space in which is the vessel
are shrunk 10 times in the sense of the movement. Idem for
time, it passes 10 times less fast inside the vessel than on the
planet Véga.
When Jaro returns on Véga, having been to look for
his plant benefactress, his journey will have been of 2 years.
Now on Véga, the time when Jaro left is of 20 years. His wife will have
aged 18 years more than him, while her daughter, now 26-year-old, will be
older than him! |
|

