Nous sommes en l'an 32 758.
Jaro, 23 ans, habite avec sa femme et sa petite fille âgée de 6 ans sur la planète Véga.
Malheureusement, un jour on lui annonce qu'il a attrapé une terrible maladie qui devrait le foudroyer dans 5 ans. Le seul
remède pour le soigner est une plante, Géromia Netsulum, qui ne pousse que sur la planète Formalhault.
Jaro, après avoir regardé sur son atlas galactique, constate que Formalhault se trouve pratiquement à 10 années-lumière de Véga. Malgré son vaisseau spatial capable d'aller jusqu'à la vitesse de 99,5% de celle de la lumière, Jaro a bien peur que le temps de voyage soit trop long. A ce rythme,
il lui faudra 10 ans pour se rendre sur Formalhault.
Pourtant,
il sait très bien qu'à cette vitesse, il ne va plus être dans la même dimension que les habitants de Véga et qu'il pourra diviser le temps du voyage et la distance séparant les deux planètes par un facteur g(gamma) grâce à la célèbre formule qu'il a apprise à l'école quand il était tout petit:
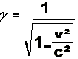
v étant la vitesse de son vaisseau
c la vitesse de la lumière
Pour ce cas de figure nous aurons cette formule:
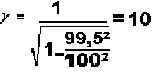
Ainsi à la vitesse de 99,5% de la lumière, le vaisseau spatial, ses occupants, tous les objets qu'il contient
y compris l'espace dans lequel se trouve le vaisseau sont rétrécis 10 fois dans le sens du déplacement. Idem pour le temps, il passe 10 fois moins vite à l'intérieur du vaisseau que sur la planète Véga.
Jaro ne mettra donc qu'une seule année pour aller sur Formalhault ce qui lui donnera largement le temps pour prendre sa plante bienfaitrice.
Lorsque Jaro reviendra sur Véga, son voyage aura été de 2 ans. Or sur Véga, le temps que Jaro est parti sera de 20 années. Sa femme aura vieilli 18 ans
de plus que lui, alors que sa fille, maintenant âgée de 26 ans, sera plus vieille que lui!
| |



